E
F
G
Geometer Sketchpad: A program published by Key Press. (http://www.keypress.com/sketchpad/) It has a lot of uses in math education, but relevant here is the fact that you can use its Iterate command (and, in older versions, the scripting feature) to draw 'simple fractals' such as the Koch Snowflake and Sierpinski Gadget.H
I
Iteration: One repetion of the mathematical process that generates a fractal. The picture resulting with 1 iteration is called '1st Iteration', the one resulting with 2 iterations is called '2nd Iteration', and so on.J
Julia set: Closely related to the Madelbrot set. Named after Gaston Julia, who , in 1917, did work on then-recently discovered complex numbers. Some starting values (in the Mandelbrot Set equation) seem to dance around the plane at random, and these lead to the cooresponding Julia sets.Jurassic Park fractal:Another name for the Dragon Curve. This term came about because Michael Crichton used various iterations of this fractal on each chapter's header page, to illustrate the role that Chaos Theory played in the book, that is, something simple rapidly becoming something incedibly complex. [Ian Malcom was a mathematician specializing in Chaos Theory, remember?] Crichton uses the 4th,5th, and 6th iterations. (which he mistakenly labels 1st,2nd,3rd)
K
Koch snowflake: A 'simple fractal' pattern that starts out with an equilateral triangle. This fractal is drawn by trisecting each side, and drawing a new equilateral triangle pointing out from the middle section. This fractal is iterated by drawing more equilateral triangles pointing out from each of the new lines. The first Koch Snowflake iteration resembles a Star of David. See also: Anti-SnowflakeL
M
Mandelbrot set: An important fractal discovered in the 1980's. It is named after its discoverer, Benoit Mandelbrot. The Mandelbrot is based on a complex number equation, and the resulting graph.Zn+1=(Zn)2+C
(Z) reprents the i-axis (vertical axis) point where a particular coordinate lies on the complex plane. C represents the real-axis point.
The answer from this equation is then used as a new input, and so on and so forth. (How many times you do this reflects the number of iterations here.)Mandelbrot sets are graphed based on what happens to each result. If the result eventually gets smaller, the point is called 'bounded', and is colored black. If it eventually gets larger, the point is called 'non-bounded', and is colored. Different colors can be used based on the rate the point result changes. Many different color patterns can be used; these color patterns create the artistic value of the Mandelbrot set. Also, you can create artistic Mandelbrots by zooming in on a particular section of the figure. Weird Mandelbrots can be created by using a different equation, such as Zn+1=(Zn)*(tangent Z)+C.
Named after Waclaw Sierpinski (1882-1969), Polish mathematician.
 Menger sponge: A cube-based fractal, wherein the center of each face of the cube is removed, creating eight small squares on the face, with the middle of each of those removed so as to continue the pattern. Much like a three-dimensional Sierpinski carpet. Aternately, you can construct a Menger sponge by taking cubes of constant size and arranging them in a way so as to mimic the pattern; an example of that can be found here: http://www.wizards.com/Magic/Magazine/Article.aspx?x=mtgcom/arcana/1569
Menger sponge: A cube-based fractal, wherein the center of each face of the cube is removed, creating eight small squares on the face, with the middle of each of those removed so as to continue the pattern. Much like a three-dimensional Sierpinski carpet. Aternately, you can construct a Menger sponge by taking cubes of constant size and arranging them in a way so as to mimic the pattern; an example of that can be found here: http://www.wizards.com/Magic/Magazine/Article.aspx?x=mtgcom/arcana/1569
N
O
Orbit:The set of answers produced by running a certain point through the mandelbrot equation.
P
Q
R
S
Sierpinski Gasket (AKA Sierpinski Triangle): Another 'simple fractal' that is based on an equilateral triangle, as is the Koch Snowflake. However, this fractal has a different process. By connecting the midpoints of the triangle's sides, you essentially divide the main triangle into one central triangle and three corner triangles. You iterate this fractal by proceeding to divide each of the corner triangles into smaller triangles themselves.
Sierpinski carpet: This fractal starts out with a dark square. You subdivide it into 9 smaller squares, 3x3. You then erase the central square. This fractal is iterated by doing the same thing in each of the edge squares, lightening their center portion.
Simple fractal: A fractal that does not involve complex numbers. These can often by drawn by had (especially for the first few iterations), and with programs such as Geometer Skketchpad.
T
U
V
W
X
Y
Z
© Alan Gilfoy, 2006
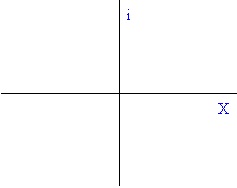 Example: 5+4i would be graphed at (5,4).
Example: 5+4i would be graphed at (5,4).